Statistics > Scatter Plot
Scatter Plot
Scatter plots show the relationship between two variables by displaying data points on a two-dimensional graph. The variable that might be considered an explanatory variable is plotted on the x axis, and the response variable is plotted on the y axis.
Scatter plots are especially useful when there is a large number of data points. They provide the following information about the relationship between two variables:
- Strength
- Shape - linear, curved, etc.
- Direction - positive or negative
- Presence of outliers
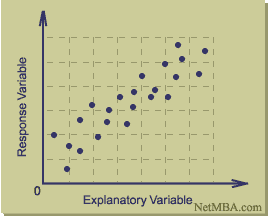
A correlation between the variables results in the clustering of data points along a line. The following is an example of a scatter plot suggestive of a positive linear relationship.
Example Scatterplot
Scatterplot Smoothing
Scatter plots may be "smoothed" by fitting a line to the data. This line attempts to show the non-random component of the association between the variables.
Smoothing may be accomplished using:
- A straight line
- A quadratic or polynomial line
- Smoothing splines - allow greater flexibility in nonlinear associations.
The curve is fitted in a way that provides the best fit, often defined as the fit that results in the minimum sum of the squared errors (least squares criterion).
The use of smoothing to separate the non-random from the random variations allows one to make predictions of the response based on the value of the explanatory variable.
Cause and Effect
When a scatter plot shows an association between two variables, there is not necessarily a cause and effect relationship. Both variables could be related to some third variable that explains their variation or there could be some other cause. Alternatively, an apparent association simply could be the result of chance.
Use of the Scatterplot
The scatter plot provides a graphical display of the relationship between two variables. It is useful in the early stages of analysis when exploring data before actually calculating a correlation coefficient or fitting a regression curve. For example, a scatter plot can help one to determine whether a linear regression model is appropriate.
Statistics > Scatterplot


