Economics > Price Elasticity of Demand
Price Elasticity of Demand
An important aspect of a product's demand curve is how much the quantity demanded changes when the price changes. The economic measure of this response is the price elasticity of demand.
Price elasticity of demand is calculated by dividing the proportionate change in quantity demanded by the proportionate change in price. Proportionate (or percentage) changes are used so that the elasticity is a unit-less value and does not depend on the types of measures used (e.g. kilograms, pounds, etc).
As an example, if a 2% increase in price resulted in a 1% decrease in quantity demanded, the price elasticity of demand would be equal to approximately 0.5. It is not exactly 0.5 because of the specific definition for elasticity uses the average of the initial and final values when calculating percentage change. When the elasticity is calculated over a certain arc or section of the demand curve, it is referred to as the arc elasticity and is defined as the magnitude (absolute value) of the following:
Q2 - Q1 |
( Q1 + Q2 ) / 2 |
P2 - P1 |
( P1 + P2 ) / 2 |
where
Q1 = Initial quantity
Q2 = Final quantity
P1 = Initial price
P2 = Final price
The average values for quantity and price are used so that the elasticity will be the same whether calculated going from lower price to higher price or from higher price to lower price. For example, going from $8 to $10 is a 25% increase in price, but going from $10 to $8 is only a 20% decrease in price. This asymmetry is eliminated by using the average price as the basis for the percentage change in both cases.
For slightly easier calculations, the formula for arc elasticity can be rewritten as:
( Q2 - Q1 ) ( P2 + P1 ) |
( Q2 + Q1 ) ( P2 - P1 ) |
To better understand the price elasticity of demand, it is worthwhile to consider different ranges of values.
Elasticity > 1
In this case, the change in quantity demanded is proportionately larger than the change in price. This means that an increase in price would result in a decrease in revenue, and a decrease in price would result in an increase in revenue. In the extreme case of near infinite elasticity, the demand curve would be nearly horizontal, meaning than the quantity demanded is extremely sensitive to changes in price. The case of infinite elasticity is described as being perfectly elastic and is illustrated below:
Perfectly Elastic Demand Curve

From this demand curve it is easy to visualize how an extremely small change in price would result in an infinitely large shift in quantity demanded.
Elasticity < 1
In this case, the change in quantity demanded is proportionately smaller than the change in price. An increase in price would result in an increase in revenue, and a decrease in price would result in a decrease in revenue. In the extreme case of elasticity near 0, the demand curve would be nearly vertical, and the quantity demanded would be almost independent of price. The case of zero elasticity is described as being perfectly inelastic.
Perfectly Inelastic Demand Curve
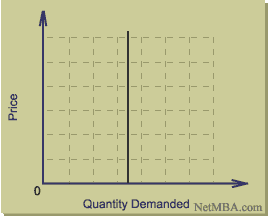
From this demand curve, it is easy to visualize how even a very large change in price would have no impact on quantity demanded.
Elasticity = 1
This case is referred to as unitary elasticity. The change in quantity demanded is in the same proportion as the change in price. A change in price in either direction therefore would result in no change in revenue.
Applications of Price Elasticity of Demand
The price elasticity of demand can be applied to a variety of problems in which one wants to know the expected change in quantity demanded or revenue given a contemplated change in price.
For example, a state automobile registration authority considers a price hike in personalized "vanity" license plates. The current annual price is $35 per year, and the registration office is considering increasing the price to $40 per year in an effort to increase revenue. Suppose that the registration office knows that the price elasticity of demand from $35 to $40 is 1.3.
Because the elasticity is greater than one over the price range of interest, we know that an increase in price actually would decrease the revenue collected by the automobile registration authority, so the price hike would be unwise.
Factors Influencing the Price Elasticity of Demand
The price elasticity of demand for a particular demand curve is influenced by the following factors:
Availability of substitutes: the greater the number of substitute products, the greater the elasticity.
Degree of necessity or luxury: luxury products tend to have greater elasticity than necessities. Some products that initially have a low degree of necessity are habit forming and can become "necessities" to some consumers.
Proportion of income required by the item: products requiring a larger portion of the consumer's income tend to have greater elasticity.
Time period considered: elasticity tends to be greater over the long run because consumers have more time to adjust their behavoir to price changes.
Permanent or temporary price change: a one-day sale will result in a different response than a permanent price decrease of the same magnitude.
Price points: decreasing the price from $2.00 to $1.99 may result in greater increase in quantity demanded than decreasing it from $1.99 to $1.98.
Point Elasticity
It sometimes is useful to calculate the price elasticity of demand at a specific point on the demand curve instead of over a range of it. This measure of elasticity is called the point elasticity. Because point elasticity is for an infinitesimally small change in price and quantity, it is defined using differentials, as follows:
dQ |
Q |
dP |
P |
and can be written as:
dQ |
P |
|
dP |
Q |
The point elasticity can be approximated by calculating the arc elasticity for a very short arc, for example, a 0.01% change in price.
Economics > Price Elasticity of Demand


